A Game Theory Model of Opportunism Behavior in Auctions

Estimated Reading Time: 19 minutes

The participants competition in the auctions, increasing complexity of how to determine the proposed price, leads the participants in the auctions to find new ways to reduce the price. One of these new methods is opportunism in announcing the price by the contractor. This means that the contractor does not consider a percentage of the price at the time of announcing the finished price with the assumption that he will be able to recover the contract amount by filing a lawsuit during the completion of the project.

If we assume that the parties act with maximum intelligence, game theory can calculate reduced amount during the price announcement . Using the game theory, we can show that after seeking opportunism in the auction, the contractor will initiate a lawsuit. The lawsuit amount depends on the conditions of the project. On the other hand, the employer, who has benefited from the initial opportunism of the contractor, tries to bargain and negotiate with the contractor.

The final equilibrium achieve and the litigation issue resolve during bargaining and the agreement of the parties. In this study, we attempted to define a game theory model for opportunism behavior in auctions. Our aim is to illustrate the ranges of agreement between parties.

Dr. Saeid HAJIHASSANIASL, Cademix Institute of Technology

A Game Theory Model of Opportunism Behavior in Auctions

Introduction

The technology progress has formed several system models like a game theory model of opportunism behavior that happens in auctions. These models in such a way that the structure of activities, behaviors and results depend on several components. The success or failure of this system depends on various elements. A game pattern defines for any type of activity and connection of a set in any structure. It is possible to change the model and generalize with the theory. Basically the game model does not have a fixed algorithm. But it forms according to the members, the way of action and other relevant and effective factors.

Game Theory, at its core, is a tool for understanding how individuals, companies, or even countries make choices. It’s like peering behind the curtain of human decision-making to discover the strategies people use to achieve their goals.

Today, we’ll embark on a journey into the realm of Game Theory, where simple choices can have complex consequences. We’ll explore a particular Game Theory model that sheds light on a common but often hidden behavior: opportunism. Specifically, we’ll delve into how opportunistic behavior can influence the outcomes of auctions.

Think of auctions as exciting events where people bid to win valuable items like art, antiques, or even houses. On the surface, they may seem straightforward: the highest bidder takes home the prize. But Game Theory shows us that it’s not always that simple. In auctions, individuals strategize, anticipate the actions of others, and sometimes resort to opportunism to gain an advantage. In this article, we’ll unpack what Game Theory is and how it can help us understand opportunistic behavior in auctions. We’ll unravel the complex web of choices and strategies that underlie these seemingly simple transactions. In this study we try to make a game theory model of opportunism behavior in auctions.

Game Theory

Game theory is a branch of applied mathematics that provides tools for analyzing situations of players decision making . In the other words, game theory is the application of mathematical models in the analysis of the behavior governing a strategic situation (the mutual influence of players’ decisions on each other) in the case of beings who think logically. These decisions are basically interdependent.

This interdependence between players makes each of them able to understand the possible strategies of another players. Each player can use it for their own strategies. Generally, game theory is a science of strategy. In other words, making the right decisions in response to competitors in a strategic space.

Using this theory, real-world scenarios for situations such as competition, pricing, product release, etc. will propose and their outcomes will predict. The aim of creating game theory is initially for understanding a large set of economic behaviors. These behaviors can be for example, fluctuations in the stock index in the stock market and fluctuations in the goods prices in the consumer market. The analysis of various economic and commercial phenomena, such as winning an auction, trading, participating in a auction, is one of the other cases in which game theory plays a role.

Today, game theory prevails in every type of interaction and communication; economic competition between two countries or two organizations; the relationship between the manager and the members or the competition of two people for the same goal. Game theory is actually a solution that describes the decisions of players in a game. These decisions may have similar, opposite or mixed interests and the outcomes that may result from these decisions. Although game theory applies for analysis between one group and multiple groups, its applications are much wider than it seems.

Game theory is a study tool for use at different levels of analysis, from economic, political and military strategies of governments to group and individual relationships. The most basic assumption of game theory is the rationality of human behavior and choices. Today, using game theory in various social, political and economic fields, including opportunism in auctions is common.

History of Game Theory

In 1921, Emile Borel started to examine a number of casino games and wrote several articles about this. In these articles, he emphasized the predictability of the results of these types of games from logical methods.

After Borel, Hungarian mathematician John von Neumann developed game theory in 1928. The reason for this was his interest in card games. Neumann realized that the outcome of this game not determined by probability theory alone. But the people involved in the game hide some information from their opponent by bluffing. In an example of the game theory application, von Neumann was able to model the actions between the United States and the Soviet Union in the Cold War. von Neumann considered them as two players in a “zero-sum game” using the strategy in the game of chess. In 1994, John Forbes Nash and two others won the Nobel Prize in Economics for their innovative studies in game theory.

Game Regions

To better define the game region, it is better to introduce the elements of the game:

Players: are the sides of the game, each of which has at least two strategies.
Strategy: an approach used to determining actions and reactions based on one’s own conditions and opponent’s movements.
Actions: It is a chain of actions that the player performs in different game situations.
Payoffs: The expected or desired profit that the player expects to get in a game.
Information: What information each player can know about the opponent’s moves at any moment of the game.
Outcome: are the results when the game ends.

Types of Games

The game theory can describe and predict the process and outcome of any type of game. This can be from a gambling game to the game in the crypto currency market. Below are some of the features by which different games are classified:

Zero-sum Game: In this game, the profit of one player is equal to the loss of another player.
Non-zero sum Game: In this game, the decisions of one player may benefit all players.
Cooperative Game: In this type of game, it is possible to compromise and collusion with others.
Non-Cooperative Game: In this type of game, there is no possibility of compromise and collusion between the participants.

How does Game Theory Work?

The game theory center is that the outcome of a player’s game depends on the strategy implemented by the others. Game theory attempts to model the behaviors governing a strategic situation. This situation arises when a person’s success depends on the strategies that others choose. The purpose of this knowledge is to find the best strategy for the players.

Game theory has a wide range of applications. This includes psychology, evolutionary biology, war, politics, economics, and business and etc. Also it analyzes the mutual logical behavior of humans, animals, and even computers.

Applications of Game Theory

Wherever people’s resources are limited and there are different options for decision-making, and there are different outputs and achievements due to different choices, or there is the possibility of cooperation and competition between actors, researcher use game theory to better analyze the situation. Game theory revolutionized economics by addressing fundamental problems in economic models. For example, neoclassical economics struggled to understand the expectation of entrepreneurship but could not cope with competition. Game theory shifted attention from steady state equilibrium to market trends. Application examples of game theory in today’s world are:

Firms’ behavior regarding product pricing under monopoly conditions.
Stock exchange transactions and crypto currencies and the reaction and decision of investors in front of market developments.
OPEC countries decides on the amount of oil extraction and oil sales and their commitment and non-commitment to the agreements.

A laziness in the global economy has led to an environment in which executive companies participate in auctions with prices lower than their minimum profit level. The reality is that the number of claims and controversies as well as their overhead costs are increasing in projects. According to Levin (1995) Claims are an inseparable part of implementation projects. Especially in projects with competitive auctions or with government financing, it is usul for the executor to participate in the auction with a low price. Because in the hope that in the future they will restore some of them through discussion and claims.

Generally, opportunism in auctions is the result of risks. It is caught in a situation of increasing costs and reducing the project profitability. Although Lannou & Leu (1993) and Kangari (1994) state that the number of claims and disputes is related to opportunism in tenders, but as Ping stated in his analytical model: we do not state that many claims are due to opportunism alone. Rather, we focus here on the fact that opportunistic behavior is related to claims.

According to Yan (2009) opportunistic behavior is a fact in most auctions. The more projects divide into smaller components and submitted to auctions, the opportunistic behavior decreases. Yan’s study points out that price competition is unable to prevent opportunistic behavior. But price competition prevents opportunism if it is accompanied by the contractor’s quality determination system. The game model for analyzing opportunism in bidding and claims will be present in this study. The purpose of presenting this model is to help project owners (employers) and executors (contractors) to understand the basic principles of the economic mechanism for filing a claim, which can itself be the basis for designing the necessary strategies in the management, planning and rules of project claims.

Game Theory Model of Opportunism Behavior

We will express the game as a dynamic game with complete information. Also we use a tree diagram to construct a game theory model for opportunism behavior in auctions . We will use the Backward Induction method to obtain the Nash equilibrium in this game. In this research all the issues will examine both from the point of view of the contractor, and the employer. In other words, although opportunism and lawsuits are considered as harmful factors for projects, the emergence of extremely competitive conditions in industrial auctions today has caused these two factors to become an inseparable part of projects.

We have presented the analysis framework of opportunism in auctions and litigation in a dynamic game in Diagram 1. In this diagram c indicates the contractor’s opportunity cost in court claims, d indicates the employer’s opportunity cost in court claims, g indicates the suggested index during negotiation, l indicates the amount of opportunistic demand by the contractor in the tender, p indicates the amount of the claim made by the contractor and q indicates the possibility of winning a court claim by contractor.

According to this diagram, the first move in this game is made by the contractor. In order to win the auction, the contractor reduces a part of the auction price by n unit and wins. In this case, the employer has received a profit of n unit, provided that the employee does not file a lawsuit until the end of the project. Therefore, the results of the contractor and the employer are (-l , l) respectively.

**Diagram 1:** Opportunistic Game with the Consequences of Different Situations

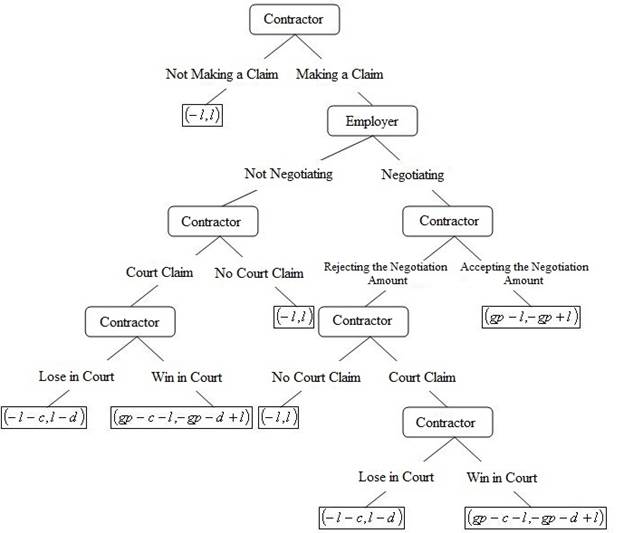
Next, it is the employer’s turn: we assume that during the project, the contractor will file a lawsuit against the employer in the amount of p units by collecting documents. So, the employer has two choices: he can start bargaining with the contractor and offer a percentage of the contract amount, such as gp units. g is a rate between zero and one. The other choice is that he chooses the solution of not discussing and bargaining and does not accept the claim plan in general.

In the continuation of the game, the third move is related to the contractor’s behavior. As we have shown in Diagram 1, if the employer decides not to negotiate, the contractor must choose whether to complain to the court or not. If the employer initiates negotiations, the issue that the contractor faces is whether to accept or reject the considered amount, that is, g must be approved by the parties during a negotiation and bargaining process. In another case, if the contractor complains to the court, according to the tree diagram, it is assumed that he will win the court with the probability q and will receive p units from the employer.

The total outcome that the contractor will get if he wins the court is p-c-l. Where c represents the opportunity cost of the contractor during the trial. The meaning of opportunity cost is the lost profit that the best possible action could have achieved for him. We should note that in this part, the only way to act is not to complain to the court. In this case, the contractor does not have to pay for the complaint to the court.

The important point is that the contractor should always pay attention to the court fees. In a complaint to the court, not only the lawyer’s fee and the court’s fees will occur, but also the court case can cause the interruption and loss of communication with the employer and therefore it will reduce the chance of working in other projects with this employer. On the other hand, if the contractor wins, the employer’s consequence will be p-d+l. Where d includes the opportunity cost of participating in court for the employer. Note that in the calculation of d, like c, indirect costs are considered.

Equilibrium in the Opportunism Behavior

We solve diagram 1 by considering the consequences of the parties from the end step by step towards the beginning. This used to construct game theory model of opportunism behavior in auctions . This method will use to solve dynamic games.

The expected consequence of the lawsuit in the court obtaining from equation 1 with the risk-neutral condition as follows:

\((q(p – c – l) + (1- q ) (- c -l ) , q (- p – d + l ) + (1 – q) (- d + l)) = (qp – c – l , – qp – d + l)\)

In this equation, the left expression shows the expected consequence of the contractor. The right side shows the expected consequence of the employer respectively.

The contractor will complain to the court in a situation where the consequence of this complaint is greater than or equal to the consequence of not complaining. As a result, the condition of making a complaint to the court by the contractor is , the result of which transferring to the previous stage. The condition for choosing a complaint in the court is as the following equation:

\(qp – c – l ≥ -l →qp≥ c\)

The game looks like Diagram 2:

**Diagram 2:** Tree Diagram with Deletion in a backward Induction Way in Game Theory Model of Opportunism Behavior

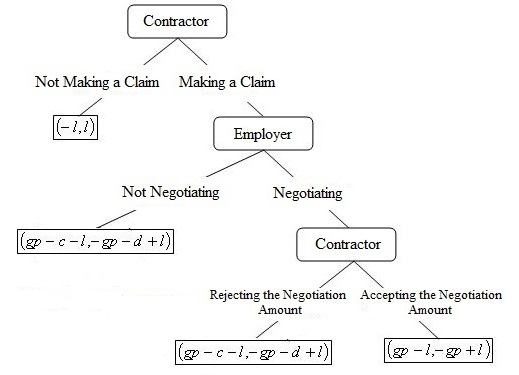
At this stage, the contractor must choose one of the options of rejecting or accepting the negotiated amount. The contractor will accept the offer as shown in the following equation:

\(gp – l ≥ qp – c – l →gp≥ qp – c \)

Regarding this condition, we can state that due to the consideration of indirect costs in the calculation of c, this number will turn into a very high amount. As a result, according to the mentioned condition, it is an acceptable condition. It seems, therefore, the diagram 3 obtains in this way:

**Diagram 3**: Tree Diagram in a Backward Induction Way in Game Theory Model of Opportunism Behavior

The meaning of last equation is that if the result expected from the lawsuit in court, qp – c , is smaller or equal to the offer presented in bargaining, gp , the contractor will accept the employer’s offer.

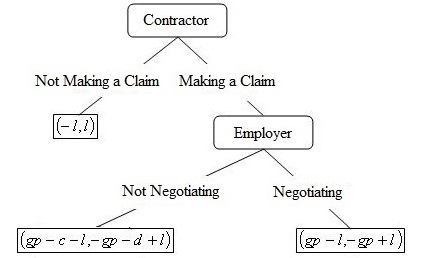
The employer has two different consequences for bargaining or not bargaining. Considering the mentioned consequences, the employer accepts to negotiate with the contractor according to the following equation:

\(-gp + l ≥ -qp – d + l → qp + d≥ qp\)

As seen in Diagram 4, the contractor will make the claim if gp – l ≥ -l . That is, the contractor will start the claim from the game under condition gp≥ 0, which is an obvious condition. So the contractor will choose the claim.

**Diagram 4**: Tree Diagram in a Backward Induction Way

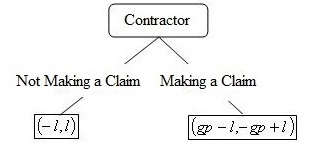
As a result, considering the mentioned conditions, the equilibrium path of the game theory model of opportunism behavior in auctions will be as follows:

Diagram 5: The Equilibrium Path of the in Game Theory Model of Opportunism Behavior

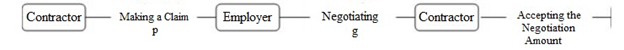
This diagram, shows the backtracking path to achieve equilibrium in each sub-game and equilibrium in the whole game. An equilibrium path means a path in which the game tree is followed at the equilibrium points. This path is unique in each sub-game. In order to express the general state of the bidding and litigation game, we first define two new parameters. Next we discuss the Nash equilibrium in the game theory model of opportunism behavior in auctions.

Probability of Wining Lawsuit in Opportunism Behavior

We assume that C is the total cost of the project. Notice that it is different from c in terms of the contractor’s opportunity cost. We define the new rate as the claim ratio, a, as the amount of the claim divided by the total cost of the project. In fact, the claim rate expresses the relationship between the claims amount reported by the contractor and the total cost of the project. It is very important that the total cost of the project means the contractor’s amount in the tender without opportunism. We can write this concept as follows:

\(P(a) = aC\)

In most projects, it is 0 ≤ a ≤ 1 , but in very rare cases of projects, it can also be 1 < a .

We introduced q as the probability of winning in court. As mentioned earlier, in this game, the parameters are related to each other. Also the amount of q is completely related to the amount of claims made by the contractor, and this amount of claims is related to the claim ratio (a). Therefore, there is a clear and obvious negative relationship between a and q. For example, for similar claims, the probability of winning in court (q) with a claim ratio of 10% must be higher than the probability of winning a claim with a claim ratio of 50%. In other words, no one can dreamily increase the amount of their litigation index without effectively reducing the probability of winning in court. Mathematically, the probability of winning in a particular court clearly expressed by a decreasing or non-increasing function of the litigation rate:

\(q(a_1)≥q(a_2)\)

where:

\(a_2≥a_1\)

In fact, a higher litigation rate reduces the probability of winning in court. So this increases the opportunity cost due to the length of the proceedings.

Expected Compensation Ratio

If the contractor files a claim in court for the amount of p and with the probability of winning q, the possible amount of compensation for his opportunism in the auction or the amount of compensation expected from the employer in favor of the contractor is the amount of qp. As a result, qp has a positive consequence for the contractor. In other side it has a negative consequence for the employer. As mentioned earlier, these parameters are completely related to the claim ratio, (a). The expected compensation ratio can be formulated as follows:

\(qp=q(a)p(a)=aq(a)C\)

We can write the expected compensation ratio in the court according to a as follows:

\(q(a)p(a)/C=aq(a)\)

Considering that the highest claim ratio (a) is a number between zero and one, the expected compensation ratio q(a) will also be in the range between zero and one. It can be seen that the obtained set is bounded. We know that in a bounded set, the existence of a maximum in the set is guaranteed. Therefore, the existence of a maximum expected compensation ratio in court for any project is guaranteed and definite. The professional lawyers are considered as experts to choose the best claim ratio in each projects.

A contractor with a logical behavior will always claim a lawsuit at the optimal ratio to maximize the overall outcome of the lawsuit. The focus of our decision-making is on the equilibrium point where the contractor decides to file a lawsuit versus not filing a lawsuit. According to the previous equations, the proposed bargaining rate should satisfy the following condition:

\(qp-c≤gp≤qp+d\)

When the contractor files a claim considering the best claim ratio, we have:

\(q(a^* )p(a^* )-c≤gp(a^* )≤q(a^* )p(a^* )+d\)

where (a^*) is the optimal claim ratio. The optimal claim ratio can be obtained by expert lawyers according to the project conditions and their experiences in similar projects, and according to that, the amount of p and q will be determined. The only variable left in the equation for both the contractor and the employer is the proposed rate in bargaining g.

Rules of the Litigation and Bidding Game

Assuming that both parties, the contractor and the employer, have natural risk tolerance and logical behavior, we state the following rules:

If the amount of expected compensation for a lawsuit in court, q(a^*)p(a^*) – c , becomes negative for contractor, then the contractor will not have incentives to be opportunistic in bidding and filing lawsuits.

If the amount of expected compensation for the lawsuit in the court, q(a^*)p(a^*) – c , is non-negative for the contractor s, the price of entering the tender can be opportunistically reduced by the contractor to the amount of l. Also, l will not be less than q(a^*)p(a^*) – c and more than q(a^*)p(a^*) + d. As a result:

\(l∈[ q(a^* )p(a^* )-c ,q(a^* )p(a^* )+d]\)

If the amount of expected compensation for the lawsuit in the court, q(a^*)p(a^*) – c, for the contractor is non-negative, negotiation and cost bargaining will lead to the best results for the employer and the contractor compared to filing a lawsuit in the court. If we consider the bargaining rate f, then f will be:

\(f∈[ q(a^* )p(a^* )-c ,q(a^* )p(a^* )+d]\)

The employer can also predict the maximum possible loss from q(a^*)p(a^*) + d by considering the worst possible case in this game. Then this is a game theory model of opportunism behavior in auctions in this research.

Conclusion and Recommendations

In this research, we decided to make a game theory model of opportunism behavior in auctions with complete information to investigate claims and opportunism in tenders. A contractor deducts some amount from the bid price at the time of bidding with the hope of filing a lawsuit in the future. In this model, we aimed to analyze the issue of opportunism in tenders and litigation by using game theory tools.

The general and real result of the model is that the Nash equilibrium of the game of litigation and bidding is negotiation and bargaining between the contractor and the employer. Based on this, the contractor reduces the price opportunistically in the period, [q(a^*)p(a^*) – c , q(a^*)p(a^*) + d] during the price offer. The mentioned period is exactly equal to the same period that the employer is willing to negotiate against the opportunism of the contractor. We saw that this interval was used when the expected compensation for the contractor was not negative in the court. Because if the expected compensation is negative, then the contractor will not have an incentive to be opportunistic in bidding and filing lawsuits.

It should be noted that obtaining real data from a project is very difficult due to the confidentiality of much information, both from the point of view of the contractor and the employer. On this basis, based on the mentioned theoretical cases, the following suggestions can be made to conduct tenders more efficiently:

Improvement as much as possible and sufficient precision in the quality of the contract and its execution by the employer.
The employer should always be ready to face any lawsuit, participate in court cases and their consequences; even the winner of the tender is the contractor whose tender price has been won without opportunism in the tender.
The employer can have a plan to get to know the contractor through various changes in the bidding procedure and its schedule by increasing relationships and also the records of previous employers and even former experts or the contractor’s subordinates.

One of the most basic strategies of the contractor is to increase productivity and accuracy in the structure of project costs.

Due to the increasing competition, the increase in filing lawsuits in case tenders is undeniable. Our game theory model of opportunism behavior in auctions found its equilibrium in negotiation and bargaining and even obtained a relatively accurate interval for the optimal amount of opportunism, the minimum reliable amount for the amount of the claim and the maximum amount of the employer’s loss. The final point that seems to be that pushing the strategy of contractors from doing opportunism in tenders to creating productivity in the structure of companies and excellent management of costs to reduce their prices and sticking to ethical issues in the economics of projects can be the most favorable suggestion for contractors.